少有人走的路最近又回顾了一遍叉积，概念我们应该了解，几何上就是向量a和b，那么向量a和b的叉积得到向量c，向量c与向量a和b相互垂直，也就是说向量c垂直于向量a和b所在的平面，同时向量c的模长等于向量a和b组成的平行四边形的面积。
物理上叉积的意义就是力矩的意义。
这里回顾一下以前写的叉积篇：叉积
实际上有个重要的问题以前忽视掉了，那就是unity左手坐标系中的叉积计算遵循左手定则，即左手微握，大拇指伸出，向量a按四指旋转方向旋转到向量b时，且小于等于180°，则向量c沿着大拇指方向，大于180°小于等于360°则与大拇指反方向，这点刚好和百度中叉积说的右手定则反过来了，验证一下也好，如下：
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class CrossTest : MonoBehaviour
{
public Transform A;
public Transform B;
private Vector3 worldCenter = Vector3.zero;
void Start()
{
}
void Update()
{
Vector3 a = A.position - worldCenter;
Vector3 b = B.position - worldCenter;
B.RotateAround(worldCenter, Vector3.up, 30.0f * Time.deltaTime);
Vector3 c = Vector3.Cross(a, b);
#if UNITY_EDITOR
Debug.DrawLine(worldCenter, A.position, Color.white);
Debug.DrawLine(worldCenter, B.position, Color.black);
Debug.DrawLine(worldCenter, c - worldCenter, Color.red);
#endif
}
}图示：
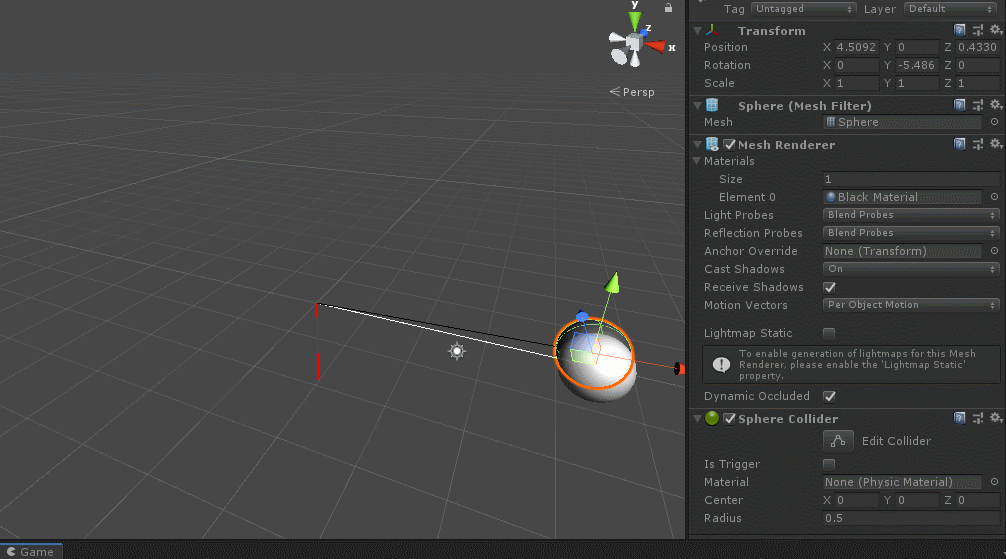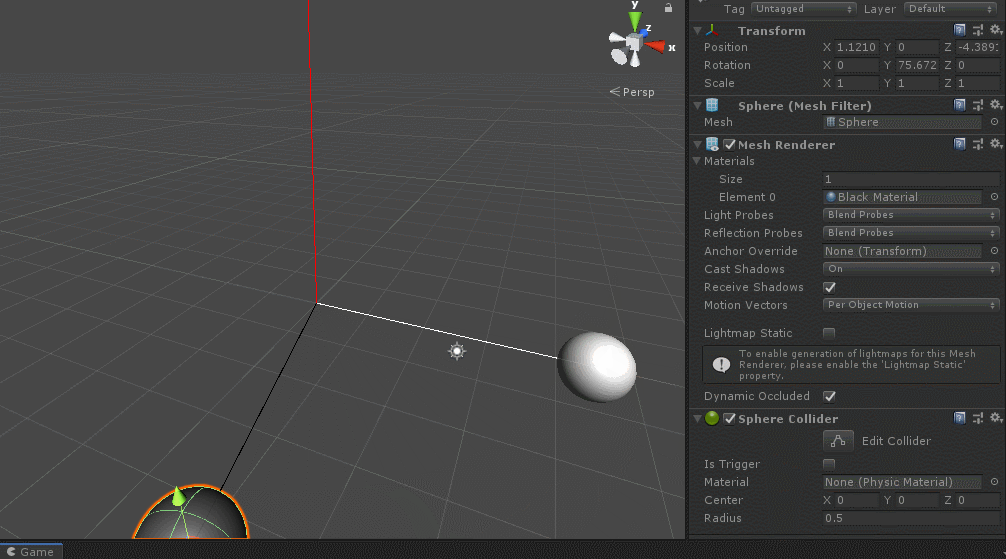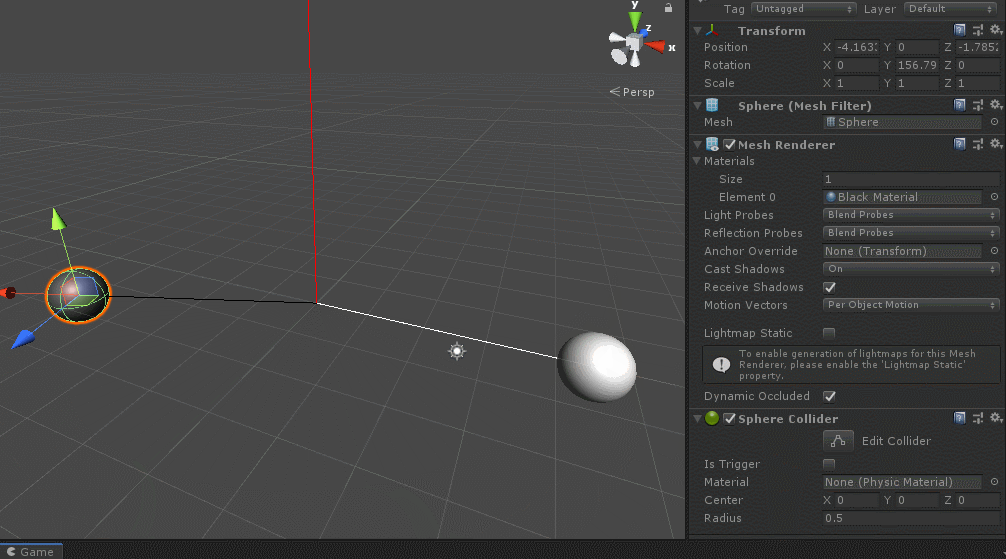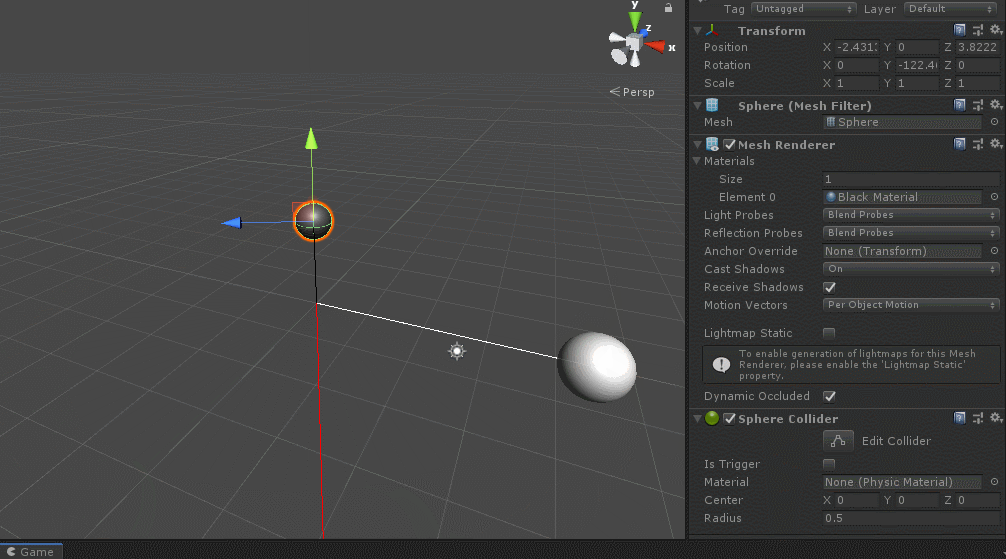
这也是unity左手坐标系中计算有符号夹角按照左手定则去判断旋转方向得到正负号。
左手微握，大拇指方向指向旋转轴方向（比如z轴），四指指向方向就是有符号正角旋转方向。
————————————————
版权声明：本文为CSDN博主「羊羊2035」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/yinhun2012/article/details/96021951
本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：
