国庆放假前写一篇,搞不好整个国庆没得机会写了,在几何开发中,点与凸多边形的关系判断属于很常见的,比如射线与平面相交,判断交点是否在若干顶点组成的多边形中。
和之前判断点在三角形中类似,先来一张点与多边形关系示意图,如下:
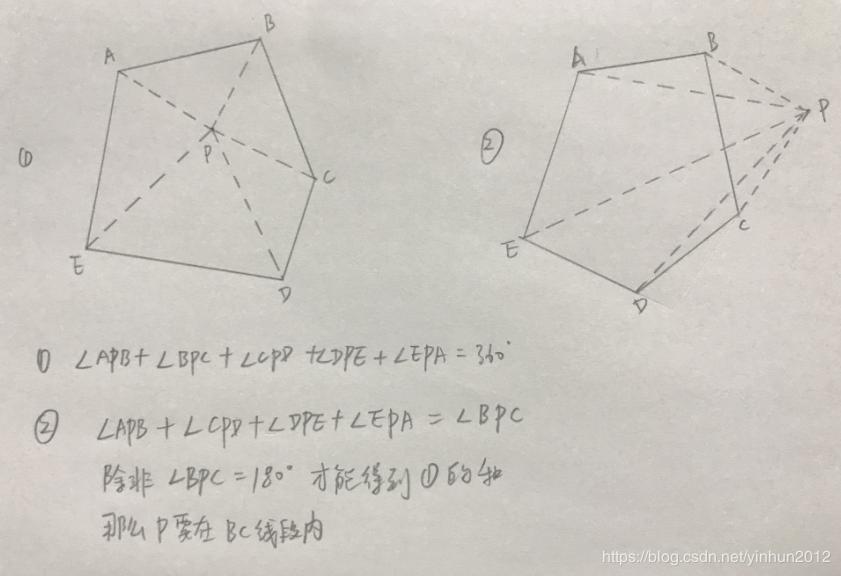
①很容易就看的出来,五个夹角之和等于360°,②可以看得出来∠BPC=其他四角之和,除非∠BPC在线段BC上,不然小于180°,则五夹角之和小于360°。
还是写程序吧,直观感受,如下:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class PointPolygon : MonoBehaviour
{
public Transform A;
public Transform B;
public Transform C;
public Transform D;
public Transform E;
public Transform P;
private Vector3 PosA;
private Vector3 PosB;
private Vector3 PosC;
private Vector3 PosD;
private Vector3 PosE;
private Vector3 PosP;
void Start()
{
}
void Update()
{
PosA = A.position;
PosB = B.position;
PosC = C.position;
PosD = D.position;
PosE = E.position;
PosP = P.position;
#if UNITY_EDITOR
Debug.DrawLine(PosA, PosB, Color.black);
Debug.DrawLine(PosB, PosC, Color.black);
Debug.DrawLine(PosC, PosD, Color.black);
Debug.DrawLine(PosD, PosE, Color.black);
Debug.DrawLine(PosE, PosA, Color.black);
#endif
bool result = CheckPointInPolygon(PosP, new Vector3[] { PosA, PosB, PosC, PosD, PosE });
#if UNITY_EDITOR
Color col = result ? Color.black : Color.red;
Debug.DrawLine(PosA, PosP, col);
Debug.DrawLine(PosB, PosP, col);
Debug.DrawLine(PosC, PosP, col);
Debug.DrawLine(PosD, PosP, col);
Debug.DrawLine(PosE, PosP, col);
#endif
}
private bool CheckPointInPolygon(Vector3 posP, Vector3[] posArr)
{
float angleSum = 0.0f;
int len = posArr.Length;
Vector3[] posCpy = new Vector3[len + 1];
System.Array.Copy(posArr, posCpy, len);
posCpy[len] = posArr[0];
for (int i = 0; i < posArr.Length; i++)
{
Vector3 a = posCpy[i] - posP;
Vector3 b = posCpy[i + 1] - posP;
float angle = Vector3.Angle(a, b);
angleSum += angle;
}
if (Mathf.Approximately(angleSum, 360.0f))
{
return true;
}
return false;
}
}效果如下:
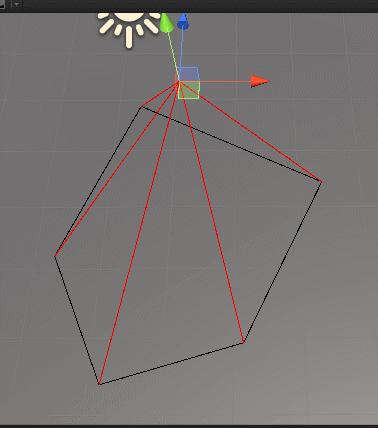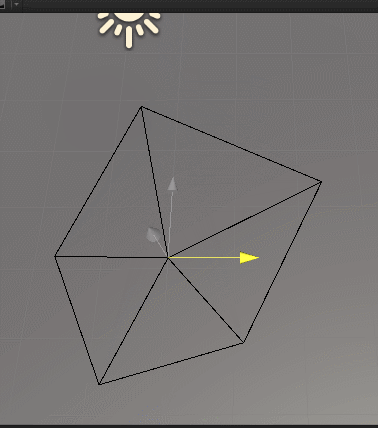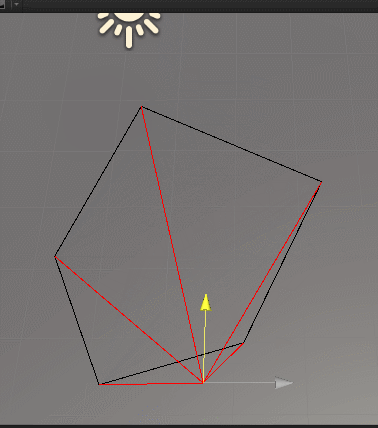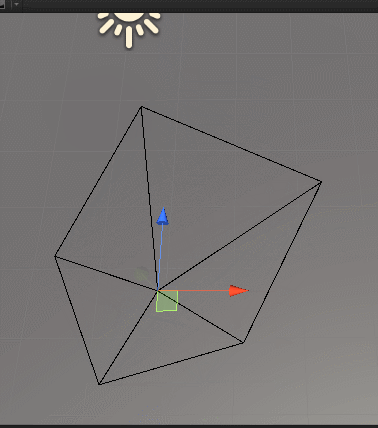
如果我们稍微仔细观察一下最开始的示意图,还会发现一点,那就是如果点在凸多边形内,那么组成的五个夹角旋转方向相同,这里我们用上左手定则,不清楚的可以回过头去看以前计算夹角的正负号问题。
通过①看得出来,假设大拇指“朝上”,∠APB、∠BPC、∠CPD、∠DPE、∠EPA都是正角,而②中则不尽然,至少∠APB、∠BPC正负号不同
那么反过来说,①中P与ABCDE组成的向量两两之间的叉积向量指向同一个方向,而②中则不同,至少向量PA与PB的叉积c1/向量PB与向量PC的叉积c2方向相反,则c1与c2的点积小于0
我们来代码实现一下:
private bool DotPointInPolygon(Vector3 pP, Vector3[] posArr)
{
Vector3[] posCpy = new Vector3[posArr.Length + 1];
System.Array.Copy(posArr, posCpy, posArr.Length);
posCpy[posArr.Length] = posArr[0];
for (int i = 0; i < posCpy.Length - 2; i++)
{
Vector3 pA = posCpy[i];
Vector3 pB = posCpy[i + 1];
Vector3 pC = posCpy[i + 2];
Vector3 PA = pA - pP;
Vector3 PB = pB - pP;
Vector3 PC = pC - pP;
Vector3 c1 = Vector3.Cross(PA, PB);
Vector3 c2 = Vector3.Cross(PB, PC);
if (Vector3.Dot(c1, c2) <= 0)
{
return false;
}
}
return true;
}来展示一下效果,如下:
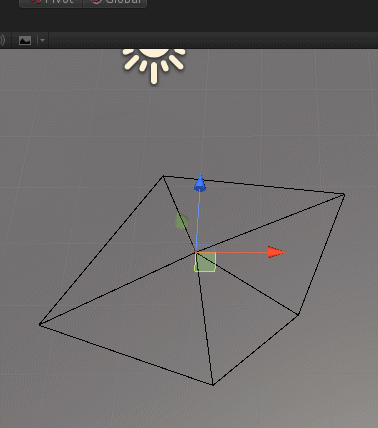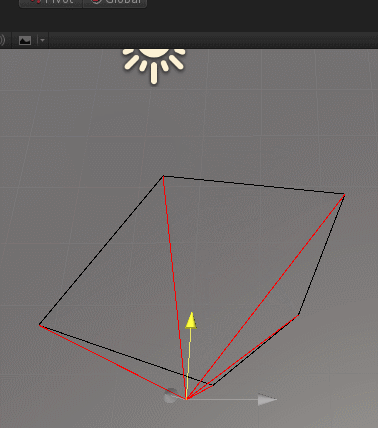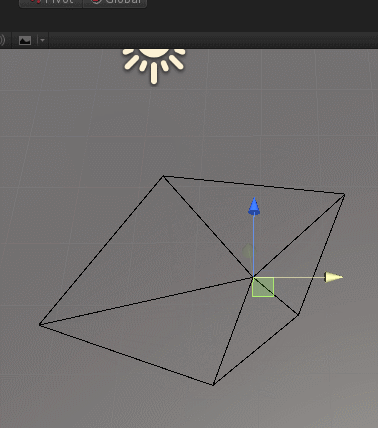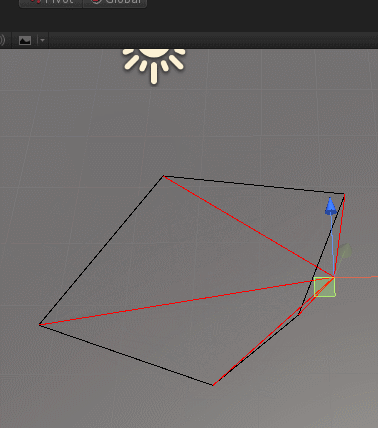
————————————————
版权声明:本文为CSDN博主「羊羊2035」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/yinhun2012/article/details/101692223

 少有人走的路
少有人走的路