少有人走的路知乎里有些扫盲贴真是精华，讲得相当通俗易懂。 把复杂的东西讲清楚也是件不容易的事，这篇文章的作者是用了真心。
简单来说，“仿射变换”就是：“线性变换”+“平移”。
先看什么是线性变换？
线性变换从几何直观有三个要点：
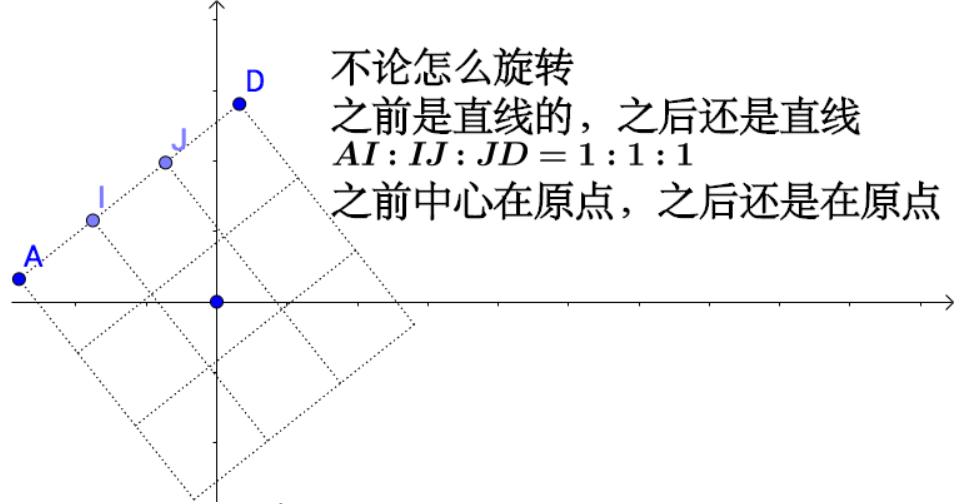
- 变换前是直线的，变换后依然是直线
- 直线比例保持不变
- 变换前是原点的，变换后依然是原点
比如说旋转
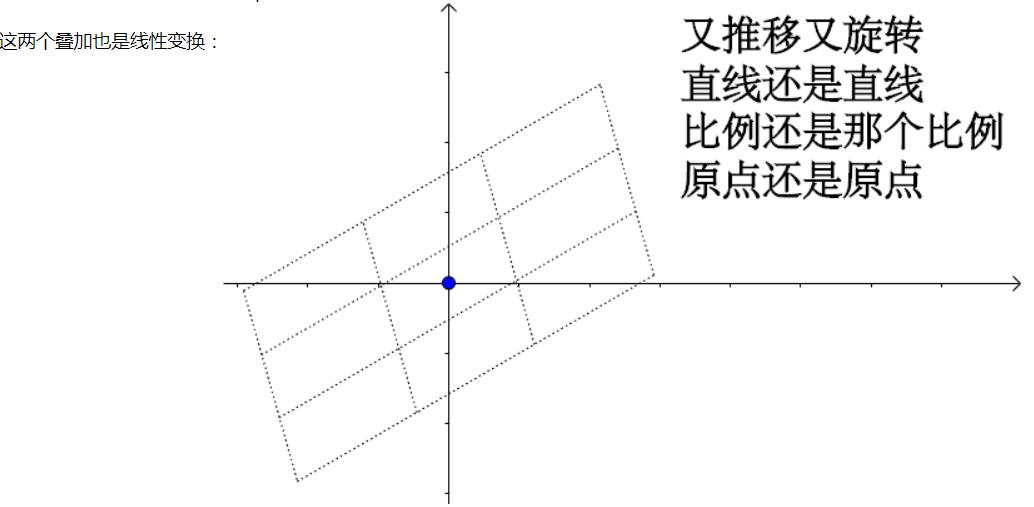
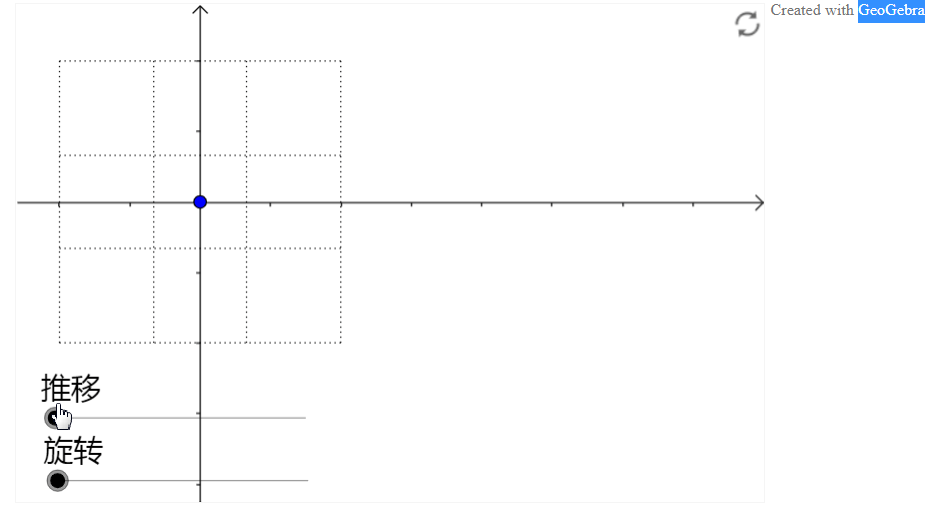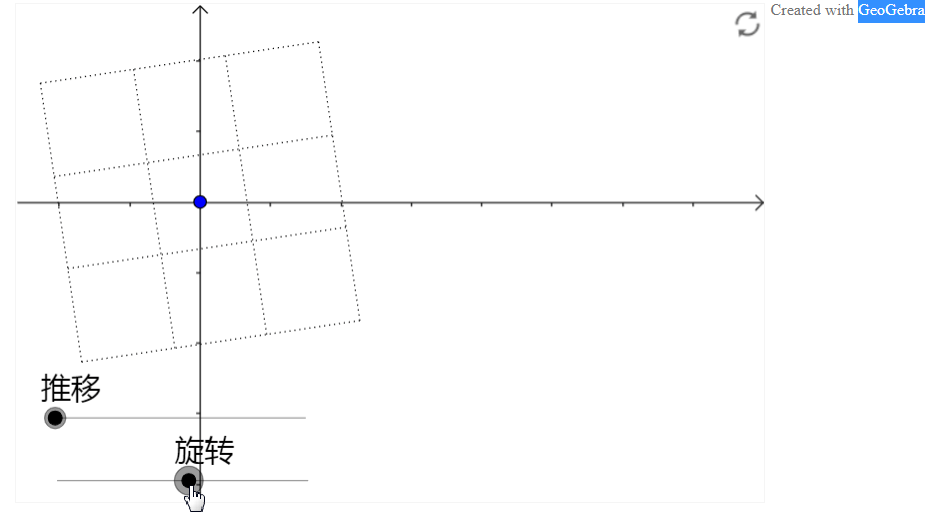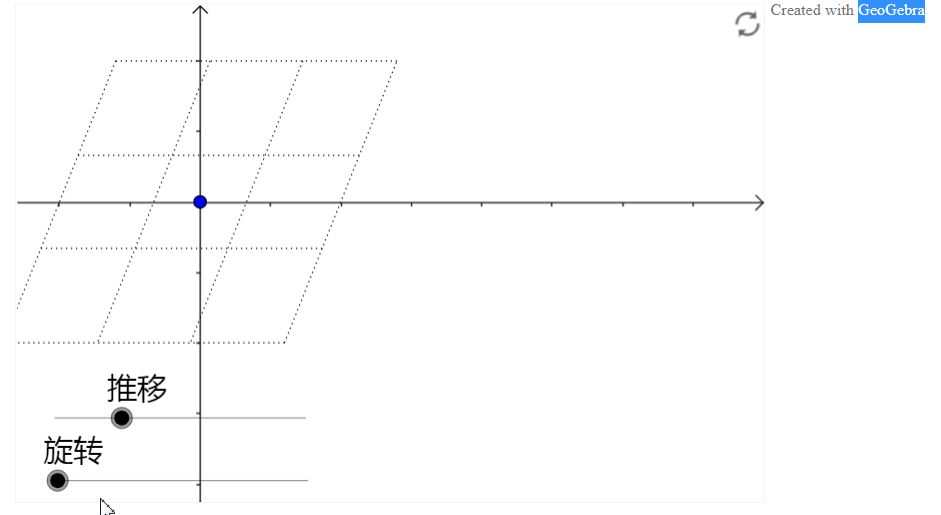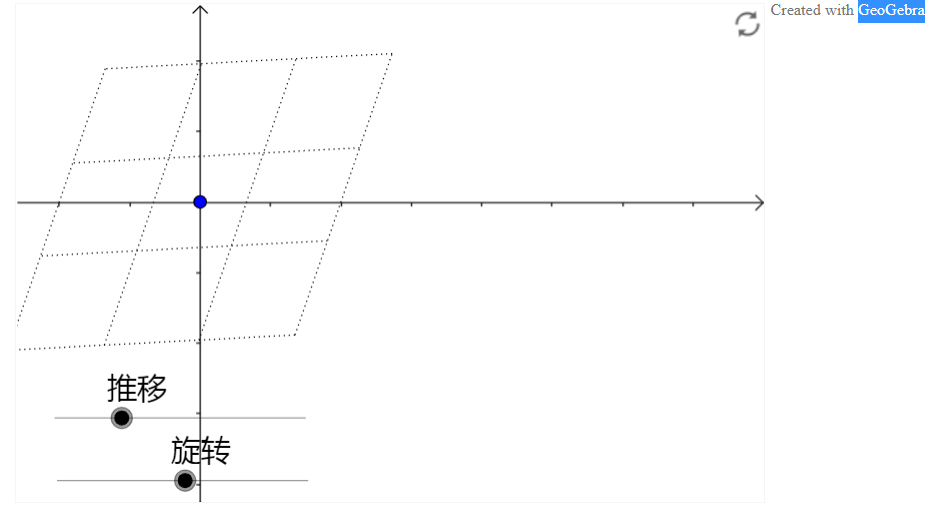
1.1 代数
简单讲一下旋转是怎么实现的，可以让我们进一步了解代数是怎么描述线性变换的。
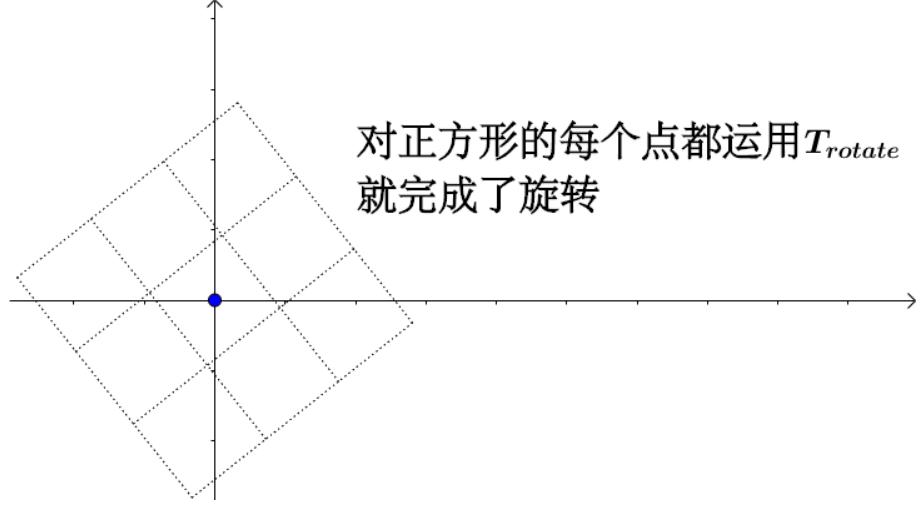
你可以手动操作下，会发现旋转矩阵在不断变化（为了方便观察旋转，我标记出一个顶点）：
总结下来，线性变换是通过矩阵乘法来实现的。
仿射变换从几何直观只有两个要点：
- 变换前是直线的，变换后依然是直线
- 直线比例保持不变
少了原点保持不变这一条。
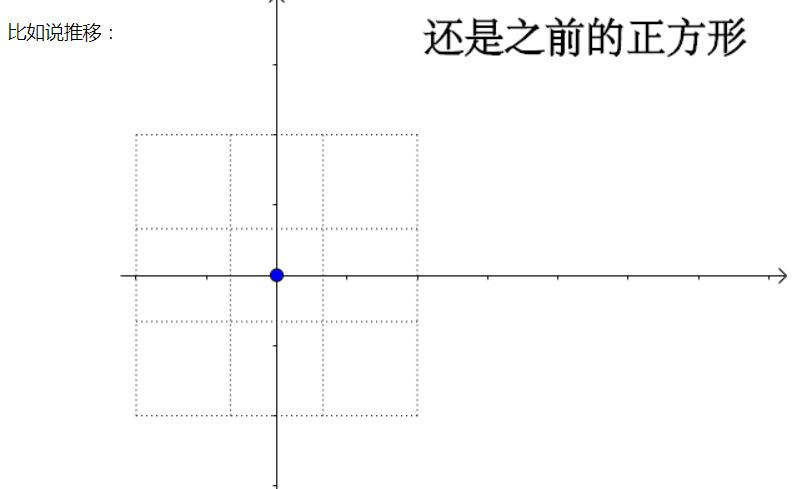
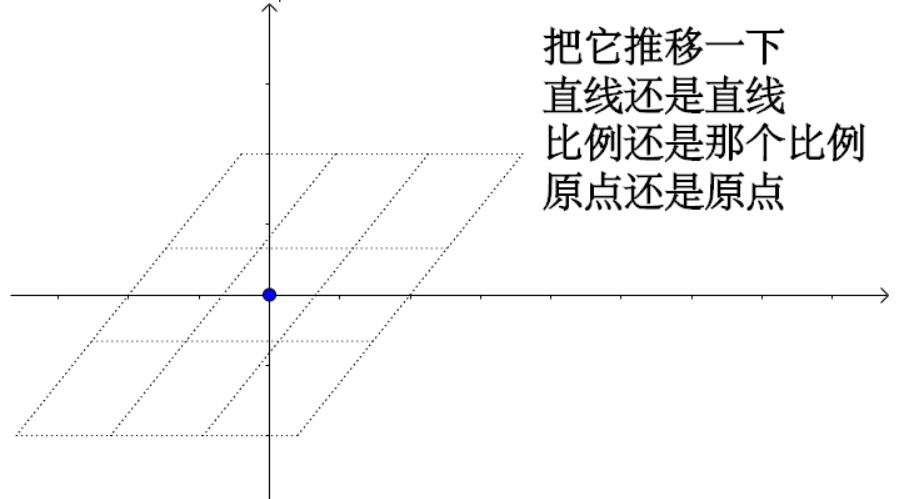
比如平移：
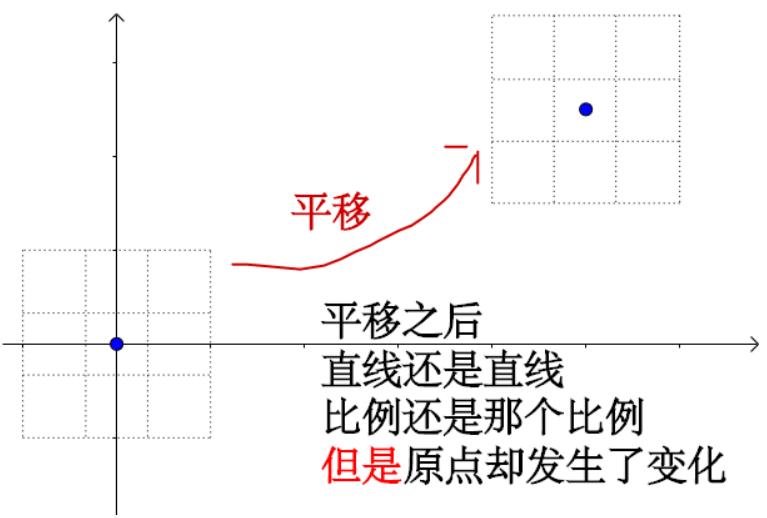
因此，平移不再是线性变化了，而是仿射变化。
2.1 代数
我们来看下仿射变换是怎么用代数来表示的。
上一节我们说了，线性变换是通过矩阵乘法来实现的，仿射变换不能光通过矩阵乘法来实现，还得有加法。
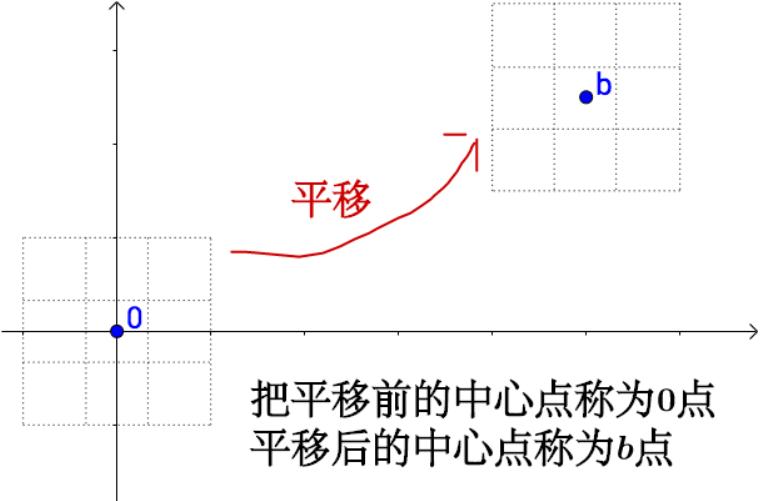
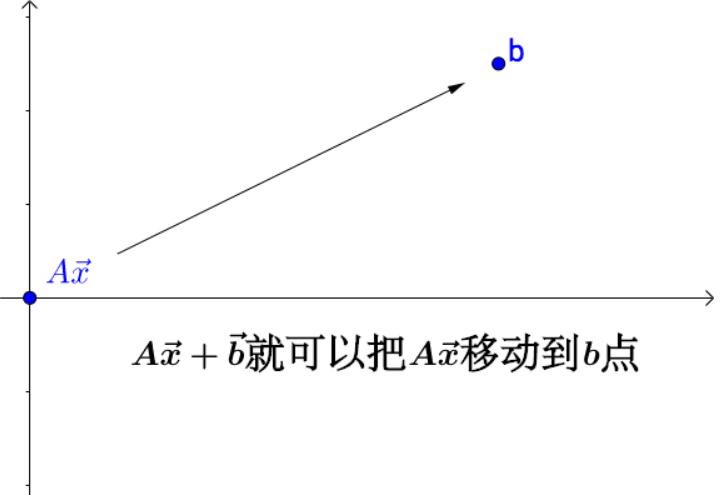
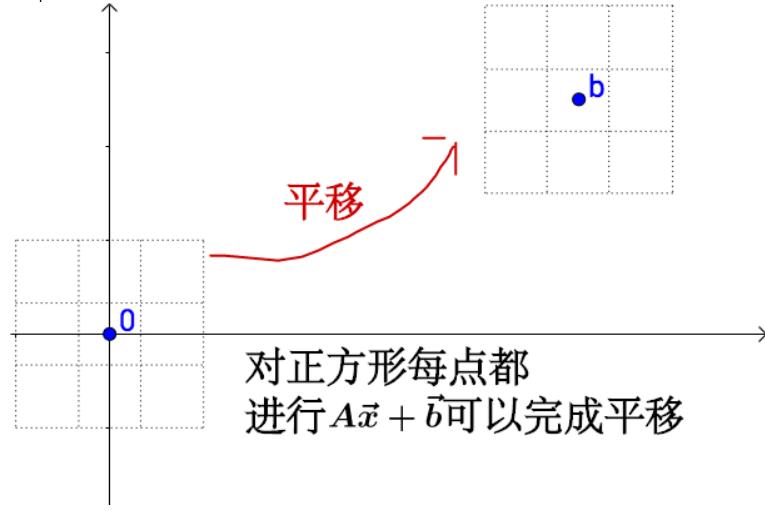
因为我们表示仿射变换为：
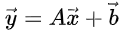
2.2 通过线性变换来完成仿射变换
这是我觉得非常优美的一个地方：
什么意思？继续举例子：
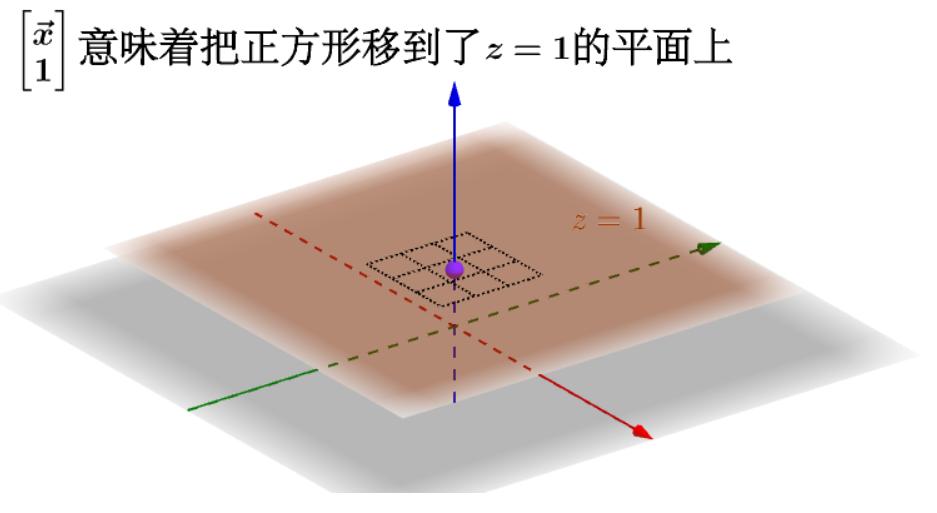
这样我就可以在三维空间下通过
这个线性变换来操作平面上的二维正方形，完成仿射变换：
自己动手操作一下：
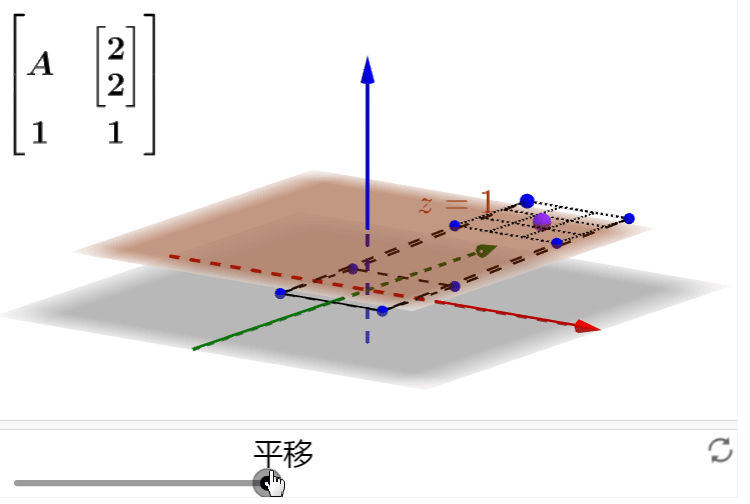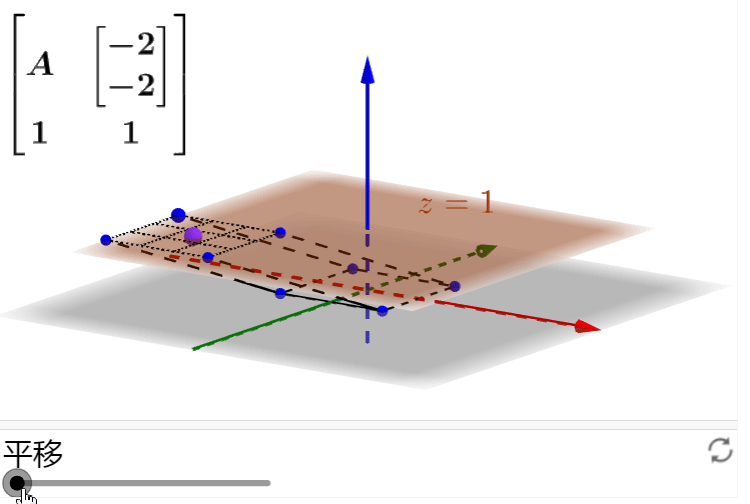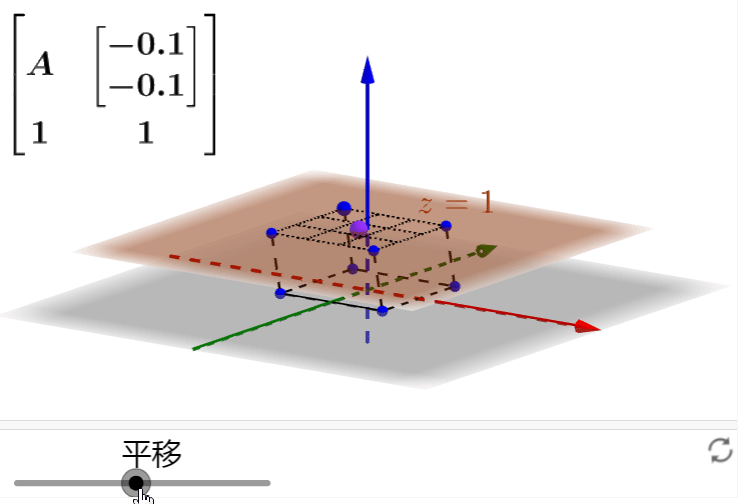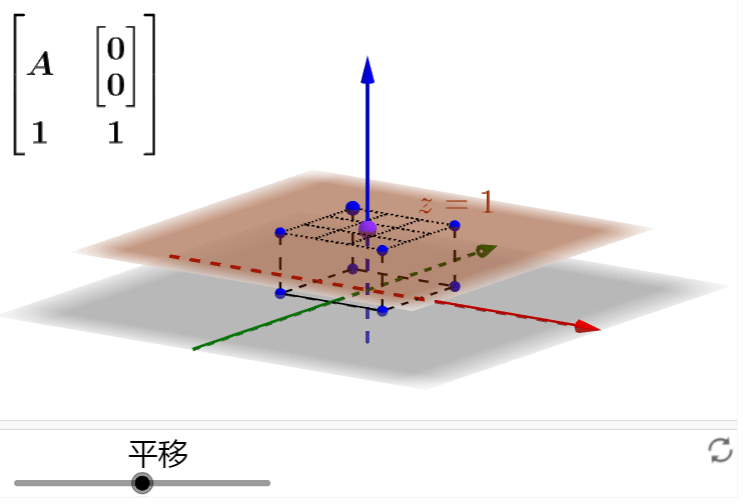
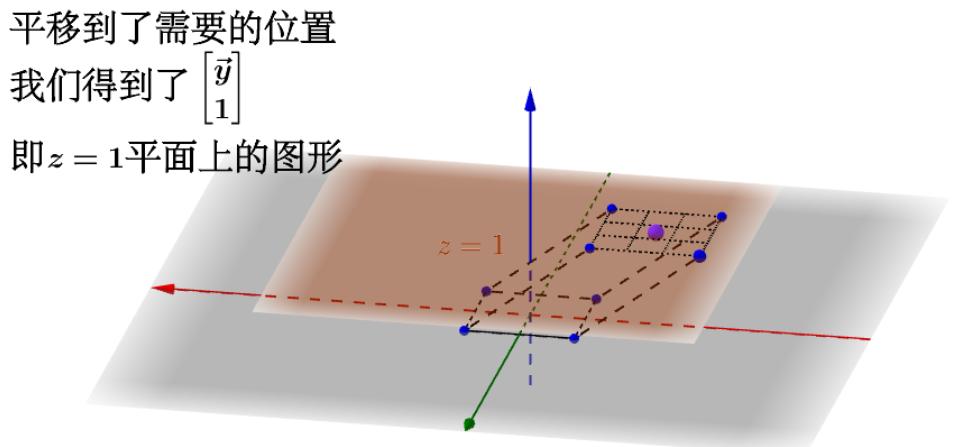
如果还有没有清楚的地方，可以结合之前的描述，看一下维基百科“仿射变换”词条里的一个gif动图，非常生动的表明了这一过程：
本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：
