少有人走的路勇哥注：
向量是unity里非常基础的一个概念，可以理解为跟3D物体的朝向有关。
标量：只有大小的量，跟其它任何性质都没关系
向量：即有大小又有方向的量
例如，你的学校在哪里？
回答：在你正前方100的地方。
这个答案就是类似向量的表示。
如果给他一个坐标位置，那这种就是标量的表示。
其它概念
向量的模：就是向量的大小，舍去方向。
单位向量：大小，或者长度为1的向量。
向量的单位化，归一化： 因为向量的大小不影响它的方向，因此有时候如果我们只对方向感兴趣，
就可以进行归一化。归一化的操作就是把向量转为单位向量。
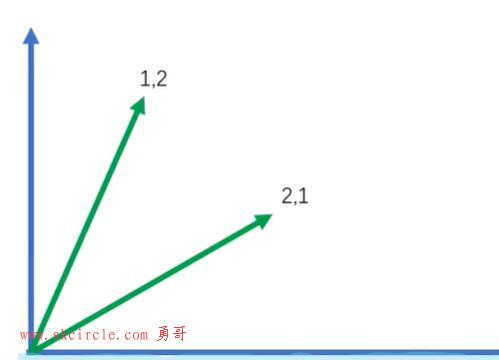
如下图：
坐标系中点的坐标表示就是向量的表示。
下面的点即有方向，也有大小
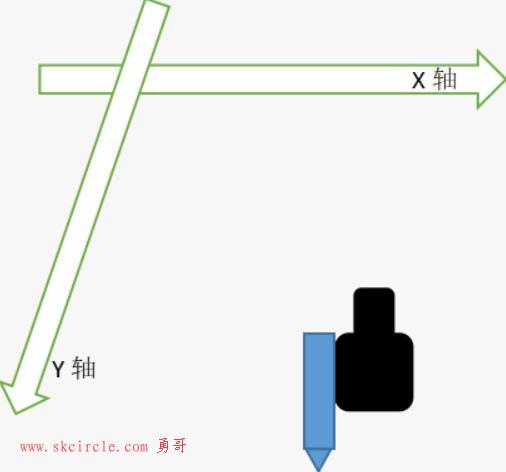
向量的作用：
圆形如果表示人，他当前看向了正前方向。
如果他想转向敌人（方块），需要求出敌人的向量，然后转向这个向量。
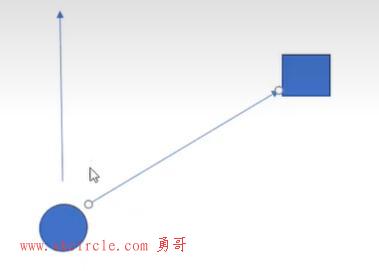
向量的运算：
(1)加法
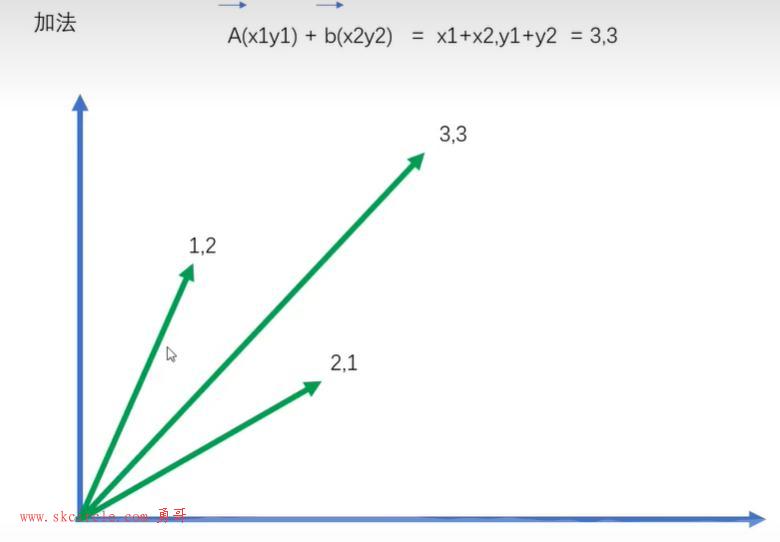
加法符合平等四边形法则。
（2）向量的减法
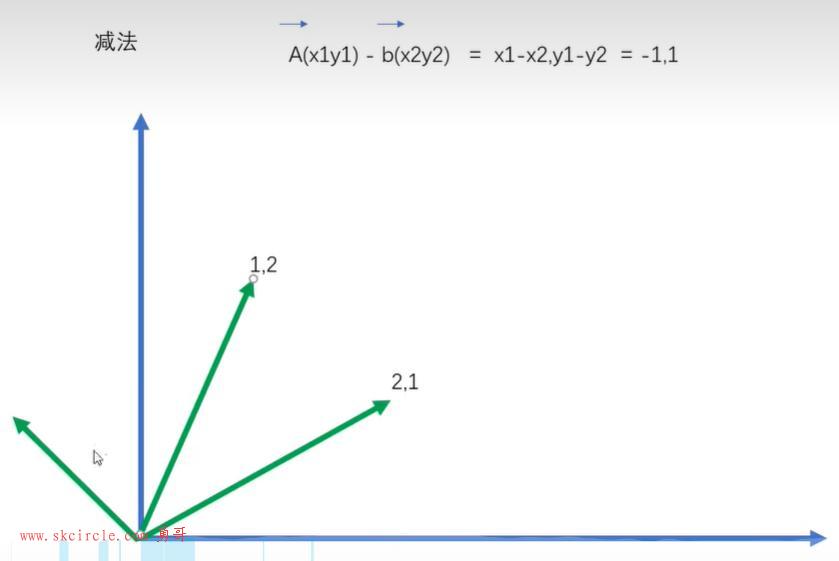
相当于直接由B向量向A向量划一条线。
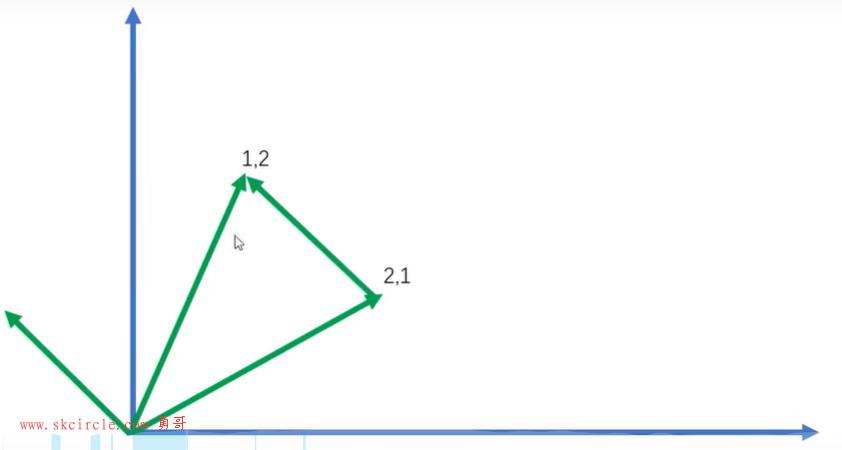
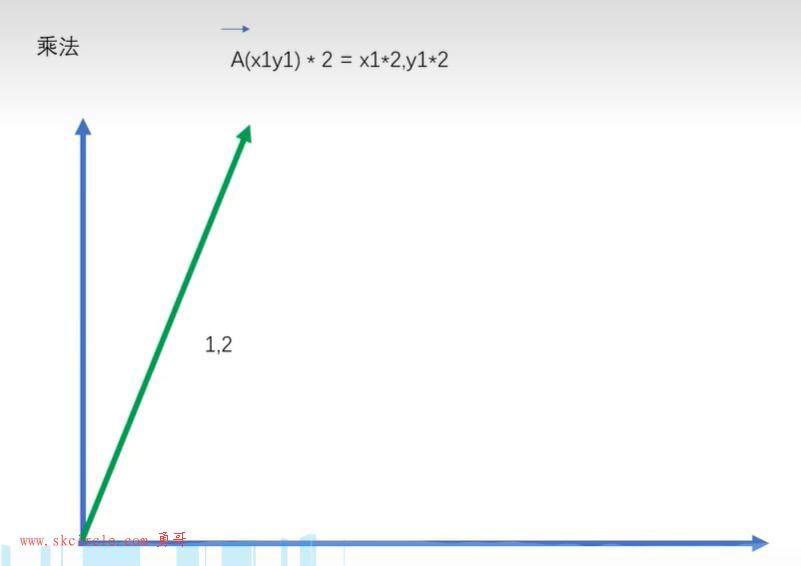
（3）向量的乘法
可以看到是一种向量和标量的运算，结果是大小变化，方向不变。
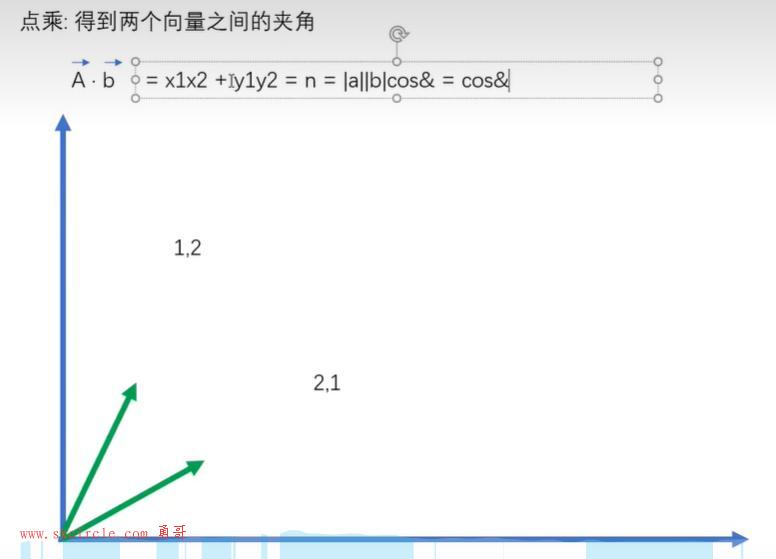
（4）点乘
它是一种非常有用的计算方式。
它可以表示为几种方式:
(1) x1x2+y1y2
(2) n 可以计算出一个值
(3) |a|.|b|. cos& （zhet）
a向量的模*B向量的模*cos（两个向量间的夹角）
引入单位向量后，简化为
n=cos&
即：cos（两个向量间的夹角）
Vector3 v=new Vector3(1,1,1);
可以表示：向量，坐标，旋转，缩放
v=Vector3.Zero
v=Vector3.one
v=Vector3.up
待续。。。。
本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：
本帖最后由 勇哥,很想停止 于 2024-10-25 10:09:24 编辑 
