SPC即统计过程控制(Statistical Process Control)。SPC主要是指应用编译分析技术对生产过程进行实时监控,科学的区分出生产过程中产品质量的随机波动与异常波动,从而对生产过程的异常趋势提出预警,以便生产管理人员及时采取措施,消除异常,恢复过程的稳定,从而达到提高和控制质量的目的。
在测量设备的软件中,经常客户的品质部门会要求设备增加SPC的相关监控工具。

计算公式举例:
过程均值 X=(X1+X2+......+Xn)/n
=(6.84+6.86+......+6.92)/25
=6.8784
平均极差 R=(R1+R2+......+Rn)/n
=(0.3*6+0.2*17+0.1*2)/25
=0.216
Uclx = X+A2R = 6.8784+0.58*0.216 = 7.0037
Lclx = X-A2R = 6.8784-0.58*0.216 = 6.7531
Uclr = D4R = 2.11*0.216 = 0.4558
Lclr = D3R = 0*0.216 = 0
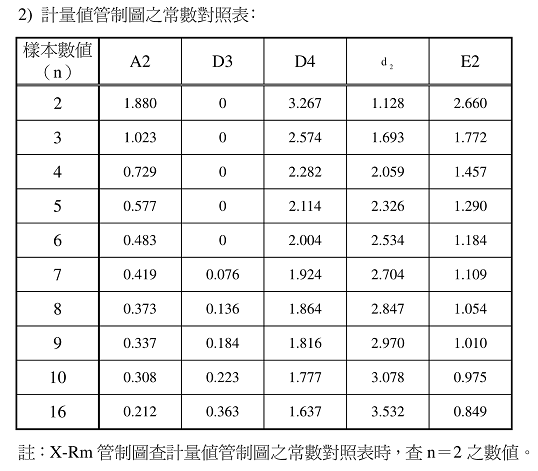
式中A2,D3,D4为常系数,决定于子组样本容量。
1其系数值见下表 :

注: 对于样本容量小于7的情况,LCLR可能技术上为一个负值。在这种情况下没有下控制限,这意味着对于一个样本数为6的子组,6个“同样的”测量结果是可能成立的。
勇哥附上一个示例,含数据:
(1)计算PT值
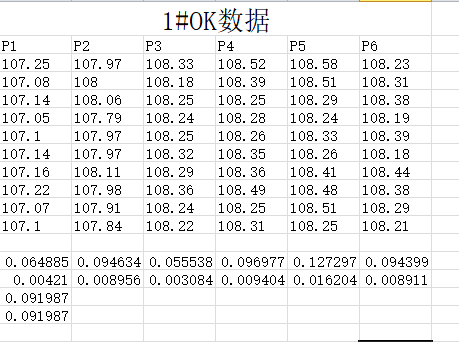
(2)计算CPK各类项目的值
| 1.65 | 1.81 | 1.65 | 1.75 | 1.7 | 1.71 | 1.49 | 1.65 | 1.65 | 1.6 | |
| 1.54 | 1.64 | 1.52 | 1.43 | 1.65 | 1.72 | 1.56 | 1.65 | 1.55 | 1.55 | |
| 1.62 | 1.51 | 1.7 | 1.62 | 1.35 | 1.75 | 1.63 | 1.75 | 1.45 | 1.65 | |
| 1.32 | 1.71 | 1.63 | 1.75 | 1.62 | 1.34 | 1.81 | 1.68 | 1.67 | 1.64 | |
| 1.61 | 1.62 | 1.78 | 1.62 | 1.65 | 1.62 | 1.65 | 1.69 | 1.63 | 1.62 | |
| 1.55 | 1.75 | 1.65 | 1.63 | 1.45 | 1.61 | 1.66 | 1.65 | 1.61 | 1.76 | |
| 1.62 | 1.58 | 1.32 | 1.57 | 1.56 | 1.65 | 1.65 | 1.75 | 1.75 | 1.85 | |
| 1.5 | 1.56 | 1.62 | 1.62 | 1.62 | 1.58 | 1.62 | 1.71 | 1.33 | 1.62 | |
| 1.6 | 1.62 | 1.61 | 1.85 | 1.62 | 1.8 | 1.43 | 1.35 | 1.25 | 1.64 | |
| 1.65 | 1.6 | 1.44 | 1.62 | 1.68 | 1.67 | 1.53 | 1.8 | 1.59 | 1.68 | |
| X否 | 1.566 | 1.64 | 1.592 | 1.646 | 1.59 | 1.645 | 1.603 | 1.668 | 1.548 | 1.661 |
| R | 0.33 | 0.3 | 0.46 | 0.42 | 0.35 | 0.46 | 0.38 | 0.45 | 0.5 | 0.3 |

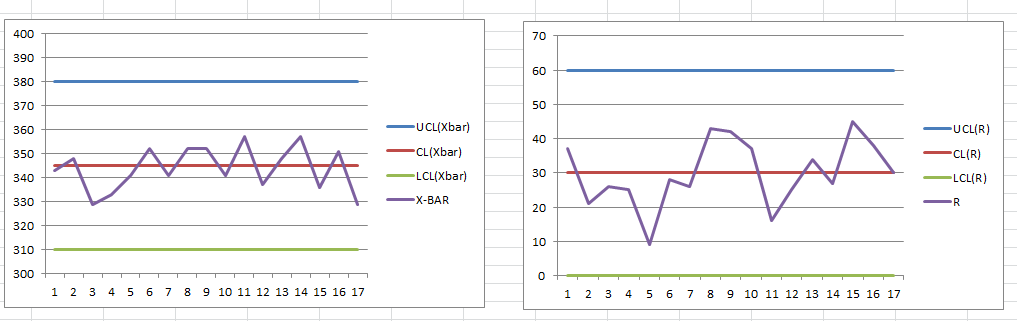
(3)画Xbar, R控制图
(4)画正态分布图
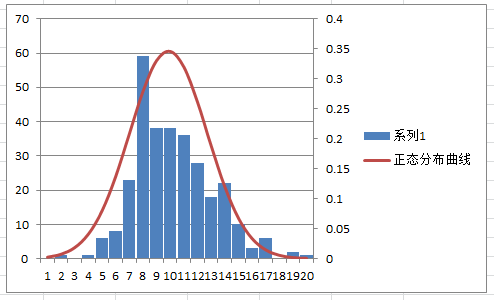
附上Excel的源文件:
另外,netMarketing类库已经包含上面各类项目的计算函数,有空勇哥会写个说明。
---------------------
作者:hackpig
来源:www.skcircle.com
版权声明:本文为博主原创文章,转载请附上博文链接!

 少有人走的路
少有人走的路