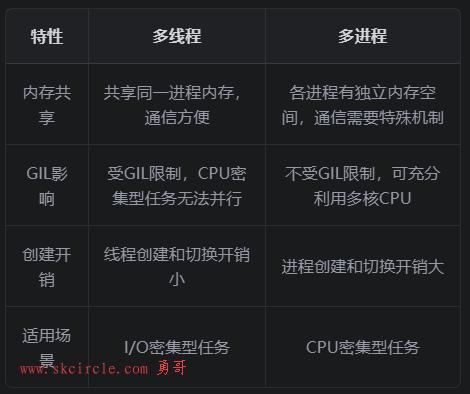
如下图,我们把角度看作是扇形的圆心角来思考,如何用长度来度量角度。
圆心角的大小与其所对应的弧度成正比,所以可以用弧长来表示角度。
在图8-10-1中,θ1:θ2=L1:L2,如果L2是K1的2倍,则圆心角θ2也是圆心角θ1的2倍。
也就是说,角度比等于弧长比。
但是,弧长本身是随扇形大小即半径不同而产生差异。这样,圆心角的度数就可以用弧长和半径的比例来表示。

如图8-10-2,同一圆心角的两个扇形互为相似形,所以,
L1/r1=L2/r2

这样,我们就得出了下面的这个公式:

这就是用弧长来计量角度的方法,称为弧度制,单位是弧度,项英文符号是rad。
当L为圆的周长时,L=2πr,所以

因为L是圆的周长,所以它对应的圆心角就是360°,这样我们就知道360°用弧度制如何表示 。

这个值是与圆的大小无关的固定数值。
相同的道理,半圆中,弧长L=PIr,所以

因为L对应的圆心角是180°

以此类推,四分之一圆,即90°时的弧度数,
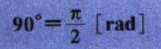
下图中,分别以30°和60°均分圆,写上了对应圆心角的弧度值:

那么问题来了, 1[rad]是多少度?
1rad意味着弧长与半径相同,即L=r。
参考图8-10-3,60°的弧度为1/3Pi,那么1rad的角度应该小于60°一点。

具体是多少度呢?我们来算一算。
1rad的弧长相当于圆周长2PIr的L/2PIr。因为L=r,所以也就是 1/2PI。
所以1rad相当于360°的1/2PI
1[rad]=360°*1/2PI=180°/PI=180°/3.1415926=57.2957795...°
反过来,1°是圆周角360的1/360,即是2PI[rad]的1/360,所以,
1°=2PI*1/360°=(PI/180)[rad]=0.01745329...[rad]
因此,一个角的度数乘以PI/180°就是这个角的弧度。
一个角的弧度数乘以180°/PI就是这个角的度数。
弧度制创立的最大理由是:正是因为有了弧度制,才能把一个角的角度和它的三角函数值放在一起作比较。
---------------------
作者:hackpig
来源:www.skcircle.com
版权声明:本文为博主原创文章,转载请附上博文链接!

 少有人走的路
少有人走的路