找线找圆是勇哥感兴趣的话题,在机器视觉里面,没有这个功能是没办法干活的。
不过,遗憾的是,勇哥按照视频里面做,曝出下面的错误。

花了几个小时网上求解,不得解,郁闷!
只能暂时先把贴子写下去,有解决办法再回来补充贴子了!
补注:2020/2/2
勇哥发现错误的原因了,我把HoughLinesP写成了HoughLines,后者是老手用的,所说要自己反变换到平面空间(暂时不懂这个)。
演示代码:
#include <opencv2/opencv.hpp>
#include <iostream>
#include <math.h>
using namespace cv;
using namespace std;
int main(int argc, char** argv) {
Mat src,gray, dst;
src = imread("e:/lines.png");
Canny(src, gray, 150, 200);
cvtColor(gray, dst, CV_GRAY2BGR);
imshow("gray", gray);
vector<Vec4f> plines;
//cvHoughLines2(&gray, &plines, 1, CV_PI / 180, 10, 0, 0);
HoughLinesP(gray, plines, 1, CV_PI / 180, 10, 0, 0);
Scalar color = Scalar(0, 0, 255);
for (size_t i = 0; i < plines.size(); i++) {
Vec4f hline = plines[i];
line(dst, Point(hline[0], hline[1]), Point(hline[2], hline[3]), color, 3, LINE_AA);
}
imshow("HoughLines", dst);
waitKey(0);
return 0;
}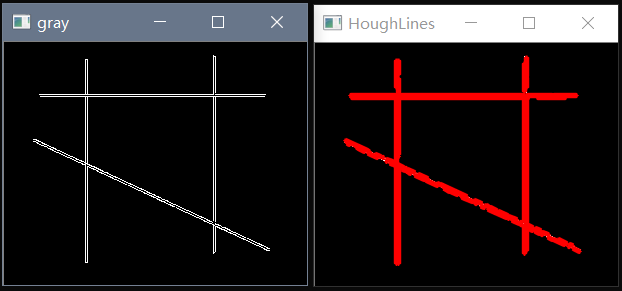
(HoughLinesP算子找线的效果)
在代码里面,勇哥很高兴看到了线上每个点的起止位置,看来接下来可以用这些点拟合出一条我们想要的直线,
这个怎么实现就是需要勇哥继续研究的话题了。
Vec4f hline = plines[i]; line(dst, Point(hline[0], hline[1]), Point(hline[2], hline[3]), color, 3, LINE_AA);
代码说明:
霍夫直线变换介绍
Hough Line Transform用来做直线检测
前提条件 – 边缘检测已经完成
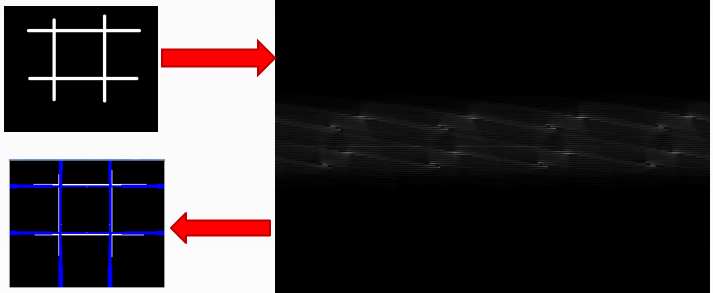
平面空间到极坐标空间转换
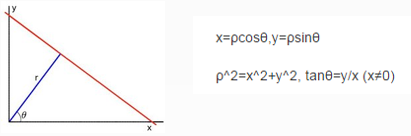
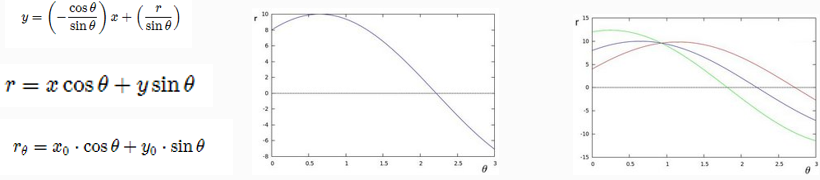
对于任意一条直线上的所有点来说
变换到极坐标中,从[0~360]空间,可以得到r的大小
属于同一条直线上点在极坐标空(r, theta)必然在一个点上有最强的信号出现,根据此反算到平面坐标中就可以得到直线上各点的像素坐标。从而得到直线
从平面坐标变换到霍夫空间(极坐标)
相关API学习
标准的霍夫变换 cv::HoughLines从平面坐标转换到霍夫空间,最终输出是
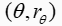 表示极坐标空间
表示极坐标空间霍夫变换直线概率 cv::HoughLinesP最终输出是直线的两个点
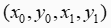
cv::HoughLines( InputArray src, // 输入图像,必须8-bit的灰度图像 OutputArray lines, // 输出的极坐标来表示直线 double rho, // 生成极坐标时候的像素扫描步长 double theta, //生成极坐标时候的角度步长,一般取值CV_PI/180 int threshold, // 阈值,只有获得足够交点的极坐标点才被看成是直线 double srn=0;// 是否应用多尺度的霍夫变换,如果不是设置0表示经典霍夫变换 double stn=0;//是否应用多尺度的霍夫变换,如果不是设置0表示经典霍夫变换 double min_theta=0; // 表示角度扫描范围 0 ~180之间, 默认即可 double max_theta=CV_PI ) // 一般情况是有经验的开发者使用,需要自己反变换到平面空间
cv::HoughLinesP( InputArray src, // 输入图像,必须8-bit的灰度图像 OutputArray lines, // 输出的极坐标来表示直线 double rho, // 生成极坐标时候的像素扫描步长 double theta, //生成极坐标时候的角度步长,一般取值CV_PI/180 int threshold, // 阈值,只有获得足够交点的极坐标点才被看成是直线 double minLineLength=0;// 最小直线长度 double maxLineGap=0;// 最大间隔 )
---------------------
作者:hackpig
来源:www.skcircle.com
版权声明:本文章代码及资料部分或全部来自贾志刚老师的视频,勇哥只是在个人理解的基础上做学习笔记,转载请附上博文链接!

 少有人走的路
少有人走的路