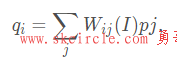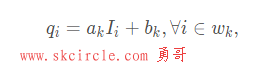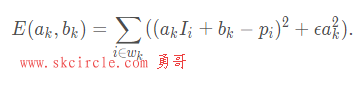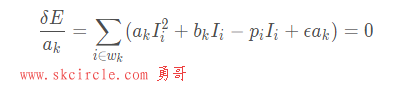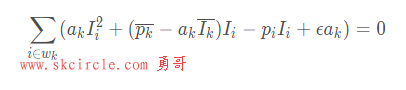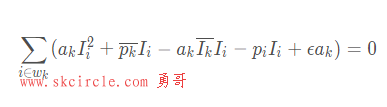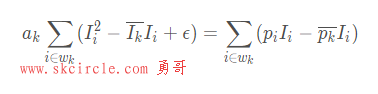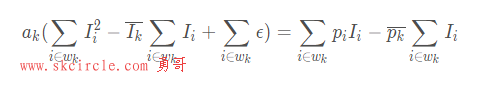引导滤波(Guided Filtering)和双边滤波(BF)、最小二乘滤波(WLS)是三大边缘保持(Edge-perserving)滤波器。当然,引导滤波的功能不仅仅是边缘保持,只有当引导图是原图的时候,它就成了一个边缘保持滤波器。
它在图像去雾,图像抠图上均有相应的应用。
原理
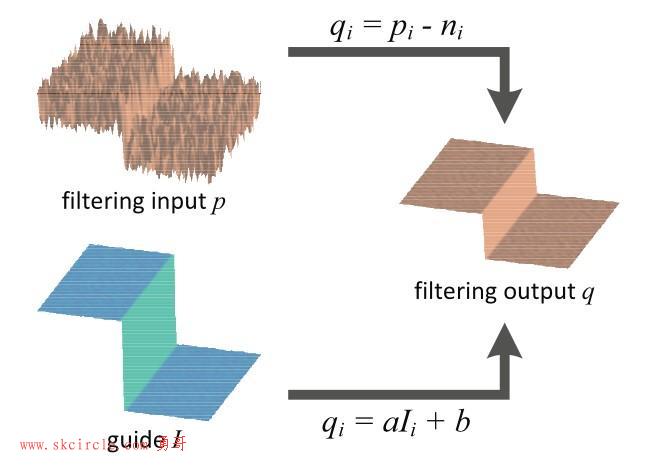
对于一个输入的图像p,通过引导图像I,经过滤波后得到输出图像q,其中p和I都是算法的输入。引导滤波定义了如下所示的一个线性滤波过程,对于i位置的像素点,得到的滤波输出是一个加权平均值:
其中,i和j分别表示像素下标。Wij是只和引导图像I相关的滤波核。该滤波器相对于p是线性的。
导向滤波的一个重要假设是输出图像q和引导图像I在滤波窗口wk上存在局部线性关系:
对于一个以r为半径的确定的窗口wk,(ak,bk)也将是唯一确定的常量系数。这就保证了在一个局部区域里,如果引导图像I有一个边缘的时候,输出图像q也保持边缘不变,因为对于相邻的像素点而言,存在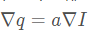 。因此只要求解得到了系数a,b也就得到了输出q。同时认为输入图像中非边缘区域又不平滑的地方视为噪声n,就有
。因此只要求解得到了系数a,b也就得到了输出q。同时认为输入图像中非边缘区域又不平滑的地方视为噪声n,就有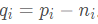 。最终的目标就是最小化这个噪声。对于每一个滤波窗口,该算法在最小二乘意义上的最优化可表示为
。最终的目标就是最小化这个噪声。对于每一个滤波窗口,该算法在最小二乘意义上的最优化可表示为
最后,引入一个正则化参数ϵ避免ak过大,得到滤波窗口内的损失函数:
求解最优化过程(对参数求偏导):
-----------------2020-10-27更新-----------------
因为求导这部分我之前也写的有问题,评论里也有问到,这里再把过程写详细点,方便大家对照自己的推导过程。
先求解bk:
为了方便运算和简化公示,这里记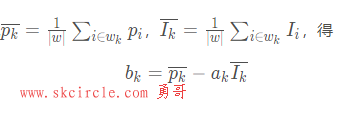
然后求解ak:
整理前面的求导公式可得:
代入简化后的bk
移项,注意求和符号的层级关系,提出ak,注意带下标k的都可以从求和函数提出:
为了进一步简化,在
即为ak的结果,相比与论文中的结果,这里进一步替换简化了公式。-----------------分割线-----------------
接下来,只要把上述线性模型应用到整个图像的滤波窗口。但是可以看到,每一个像素点会被包含在多个窗口里。比如,如果用3*3的窗口滤波,那么除了边缘区域的每个点都会被包含在9个窗口里。因此,对于不同的窗口,我们将会得到∣w∣个qi值,就对所有的qi值取平均,得到最终结果:
边缘保持
对于该算法,当I=p时,即输入图像和引导图像是同一副图像时,该算法即成为一个边缘保持滤波器。同时,方程的解也可作如下表示: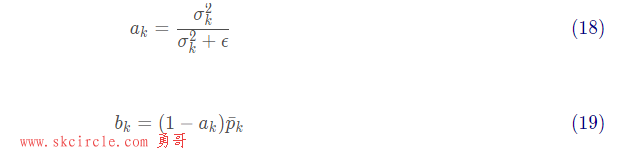
从中可以看出,ϵ在这里相当于界定平滑区域和边缘区域的阈值。
考虑以下两种情况:
应用
1、以自身作为引导图的保边平滑滤波:
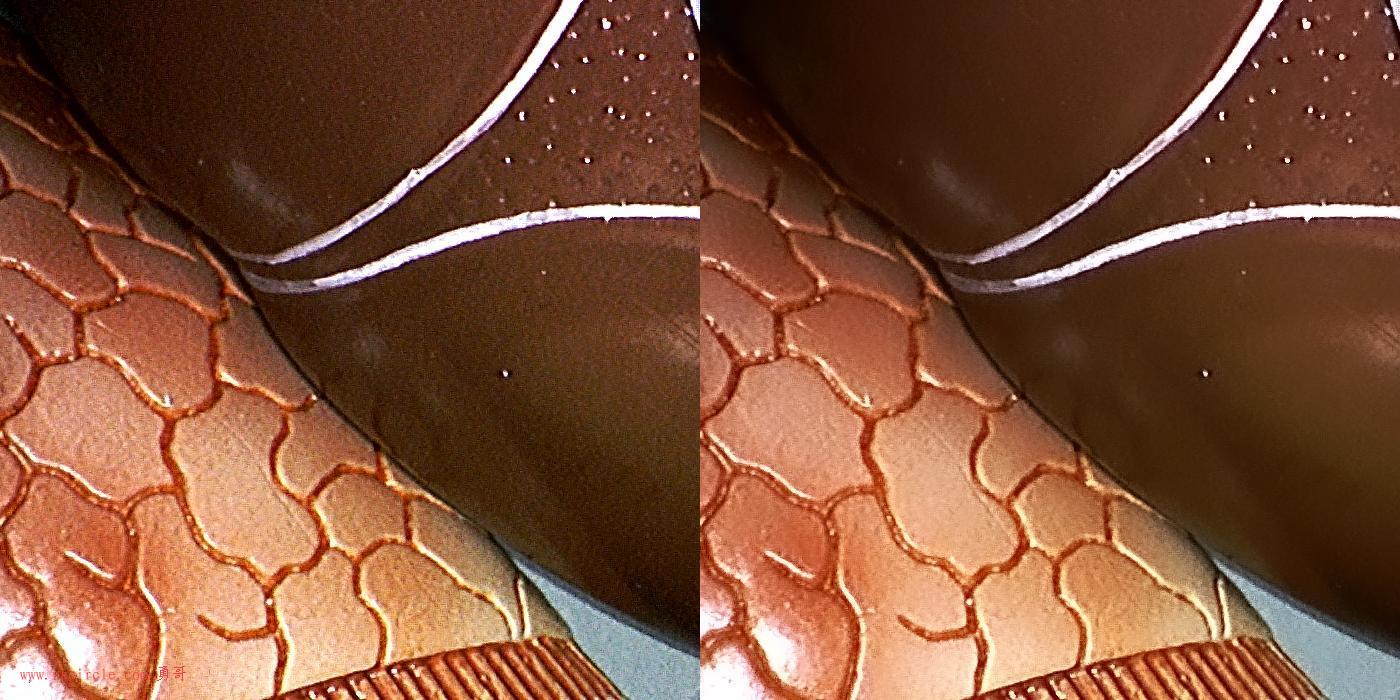
2、以原图引导的对透射率滤波的暗通道去雾
3、以原图引导的对权重图滤波的引导图像融合
转载自:https://blog.csdn.net/weixin_43194305/article/details/88959183

 少有人走的路
少有人走的路