各向异性扩散滤波主要是用来平滑图像的,克服了高斯模糊的缺陷,各向异性扩散在平滑图像时是保留图像边缘的,和双边滤波很像。
通常我们有将图像看作矩阵的,看作图的,看作随机过程的,记得过去还有看作力场的。这次新鲜,将图像看作热量场了。每个像素看作热流,根据当前像素和周围像素的关系,来确定是否要向周围扩散。比如某个邻域像素和当前像素差别较大,则代表这个邻域像素很可能是个边界,那么当前像素就不向这个方向扩散了,这个边界也就得到保留了。
具体的推导公式都是热学上的,自己也不太熟悉,感兴趣的可以去看原论文,引用量超7000吶。我这里只介绍一下最终结论用到的公式。
主要迭代方程如下:
主要迭代方程如下:
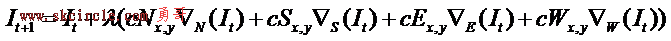
I就是图像了,因为是个迭代公式,所以有迭代次数t。
四个散度公式是在四个方向上对当前像素求偏导,news就是东南西北嘛,公式如下:
四个散度公式是在四个方向上对当前像素求偏导,news就是东南西北嘛,公式如下:

而cN/cS/cE/cW则代表四个方向上的导热系数,边界的导热系数都是小的。公式如下:
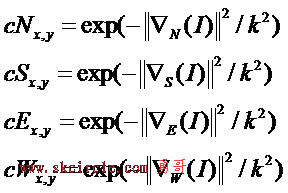
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
float k = 15;
float lambda = 0.25;
int N = 20;
void anisotropy_demo(Mat &image, Mat &result);
int main1(int argc, char** argv) {
Mat src = imread("3992.jpg");
if (src.empty()) {
printf("could not load image...\n");
return -1;
}
namedWindow("input image", CV_WINDOW_AUTOSIZE);
imshow("input image", src);
vector<Mat> mv;
vector<Mat> results;
split(src, mv);
for (int n = 0; n < mv.size(); n++) {
Mat m = Mat::zeros(src.size(), CV_32FC1);
mv[n].convertTo(m, CV_32FC1);
results.push_back(m);
}
int w = src.cols;
int h = src.rows;
Mat copy = Mat::zeros(src.size(), CV_32FC1);
for (int i = 0; i < N; i++) {
anisotropy_demo(results[0], copy);
copy.copyTo(results[0]);
anisotropy_demo(results[1], copy);
copy.copyTo(results[1]);
anisotropy_demo(results[2], copy);
copy.copyTo(results[2]);
}
Mat output;
normalize(results[0], results[0], 0, 255, NORM_MINMAX);
normalize(results[1], results[1], 0, 255, NORM_MINMAX);
normalize(results[2], results[2], 0, 255, NORM_MINMAX);
results[0].convertTo(mv[0], CV_8UC1);
results[1].convertTo(mv[1], CV_8UC1);
results[2].convertTo(mv[2], CV_8UC1);
Mat dst;
merge(mv, dst);
imshow("result", dst);
imwrite("result.jpg", dst);
waitKey(0);
return 0;
}
void anisotropy_demo(Mat &image, Mat &result) {
int width = image.cols;
int height = image.rows;
// 四邻域梯度
float n = 0, s = 0, e = 0, w = 0;
// 四邻域系数
float nc = 0, sc = 0, ec = 0, wc = 0;
float k2 = k*k;
for (int row = 1; row < height - 1; row++) {
for (int col = 1; col < width - 1; col++) {
// gradient
n = image.at<float>(row - 1, col) - image.at<float>(row, col);
s = image.at<float>(row + 1, col) - image.at<float>(row, col);
e = image.at<float>(row, col - 1) - image.at<float>(row, col);
w = image.at<float>(row, col + 1) - image.at<float>(row, col);
nc = exp(-n*n / k2);
sc = exp(-s*s / k2);
ec = exp(-e*e / k2);
wc = exp(-w*w / k2);
result.at<float>(row, col) = image.at<float>(row, col) + lambda*(n*nc + s*sc + e*ec + w*wc);
}
}
}
void anisotropic_diffusion(cv::Mat &out, cv::Mat &in, int k, float lambda);
void anisotropic_diffusion(cv::Mat &out, cv::Mat &in, int k, float lambda)
{
int i, j;
int iter = 20;
int nRow = in.rows, nCol = in.cols;
float ei, si, wi, ni;
float ce, cs, cw, cn;
cv::Mat tmp = in.clone();
uchar *pin = in.data;
uchar *ptmp = tmp.data;
uchar *pout = out.data;
for (int n = 0; n < iter; n++)
{
for (i = 1; i < nRow - 1; i++)
for (j = 1; j < nCol - 1; j++)
{
float cur = ptmp[i*nCol + j];
ei = ptmp[(i - 1)*nCol + j] - cur;
si = ptmp[i*nCol + j + 1] - cur;
wi = ptmp[(i + 1)*nCol + j] - cur;
ni = ptmp[i*nCol + j - 1] - cur;
ce = exp(-ei*ei / (k*k));
cs = exp(-si*si / (k*k));
cw = exp(-wi*wi / (k*k));
cn = exp(-ni*ni / (k*k));
pout[i*nCol + j] = cur + lambda*(ce*ei + cs*si + cw*wi + cn*ni);
}
out.copyTo(tmp);
}
}
int main(int argc, char** argv) {
Mat src = imread("3992.jpg",0);
if (src.empty()) {
printf("could not load image...\n");
return -1;
}
namedWindow("input image", CV_WINDOW_AUTOSIZE);
imshow("input image", src);
Mat dst = src.clone();
double t1 = getTickCount();
int k = 15;
float lambda = 0.25;
anisotropic_diffusion(dst, src, k, lambda);
double t2 = getTickCount();
cout << (t2 - t1) / getTickFrequency() * 1000 << endl;
imshow("result", dst);
imwrite("result.jpg", dst);
waitKey(0);
return 0;
}MATLAB仿真代码
clear all;
close all;
clc;
k=15; %导热系数,控制平滑
lambda=0.15; %控制平滑
N=20; %迭代次数
img=double(imread('lena.jpg'));
imshow(img,[]);
[m n]=size(img);
imgn=zeros(m,n);
for i=1:N
for p=2:m-1
for q=2:n-1
%当前像素的散度,对四个方向分别求偏导,局部不同方向上的变化量,
%如果变化较多,就证明是边界,想方法保留边界
NI=img(p-1,q)-img(p,q);
SI=img(p+1,q)-img(p,q);
EI=img(p,q-1)-img(p,q);
WI=img(p,q+1)-img(p,q);
%四个方向上的导热系数,该方向变化越大,求得的值越小,从而达到保留边界的目的
cN=exp(-NI^2/(k*k));
cS=exp(-SI^2/(k*k));
cE=exp(-EI^2/(k*k));
cW=exp(-WI^2/(k*k));
imgn(p,q)=img(p,q)+lambda*(cN*NI+cS*SI+cE*EI+cW*WI); %扩散后的新值
end
end
img=imgn; %整个图像扩散完毕,用已扩散图像的重新扩散。
end
figure;
imshow(imgn,[]);
转载自:
https://blog.csdn.net/sinat_36412790/article/details/80414794
本文出自勇哥的网站《少有人走的路》wwww.skcircle.com,转载请注明出处!讨论可扫码加群:


 少有人走的路
少有人走的路