少有人走的路三点确定一个圆的计算方法
最近在写的一个软件需要根据三个坐标点来计算一个圆。因此花了点时间推导了相关的公式。这个推导不算太难，放在这里主要是做个备忘。
我们设一个圆的圆心坐标为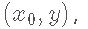 
，半径为 r 。那么这个圆的方程可以写为：
在这个圆上随便取三个点，设这三个点的坐标分别是 
那么有：
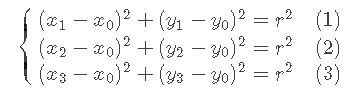
公式（1）（2）相减，（1）（3）相减之后经过化简可以得到：
有唯一解的条件是系数行列式不为 0 ：
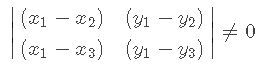
简单变变型也就是：
这样写几何含义就很明显了，三点不能共线。
设: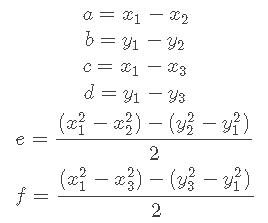
那么 :
有了 x 0 和 y 0 的值后，带入(1) 式就可以得到 r 的值。至此，三点确定圆的问题就解决了。
下面是个 C++ 代码（用到了Qt 的 QPointF 类型）：
#include <math.h>
#include <limits>
#include <QPoint>
#include <QDebug>
QPointF tcircle(QPointF pt1, QPointF pt2, QPointF pt3, double &radius)
{
double x1 = pt1.x(), x2 = pt2.x(), x3 = pt3.x();
double y1 = pt1.y(), y2 = pt2.y(), y3 = pt3.y();
double a = x1 - x2;
double b = y1 - y2;
double c = x1 - x3;
double d = y1 - y3;
double e = ((x1 * x1 - x2 * x2) + (y1 * y1 - y2 * y2)) / 2.0;
double f = ((x1 * x1 - x3 * x3) + (y1 * y1 - y3 * y3)) / 2.0;
double det = b * c - a * d;
if( fabs(det) < 1e-5)
{
radius = -1;
return QPointF(0,0);
}
double x0 = -(d * e - b * f) / det;
double y0 = -(a * f - c * e) / det;
radius = hypot(x1 - x0, y1 - y0);
return QPointF(x0, y0);
}勇哥2020/8/9注：
hypot函数头文件math.h或cmath
hypot(a,b)的返回值为double类型，相当于sqrt(a*a+b*b)
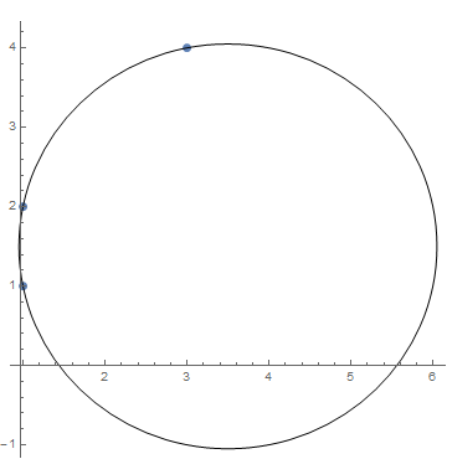
用 {1, 1}, {1, 2}, {3, 4} 这三个点测试了一下。结果没有问题。
本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：
