少有人走的路我们知道，振幅就是振动中心到最高点或者最低点的长度。如果改变一个函数图象的振幅、移动它的中心，图象会变成什么样呢？
例子： 比较函数y=2sinθ和函数y=sinθ的图象。
如下图，y坐标表示图象的高低。把y=sinθ的图象的高度沿着y轴上下伸长两倍，就得到了y=2sinθ的图象。
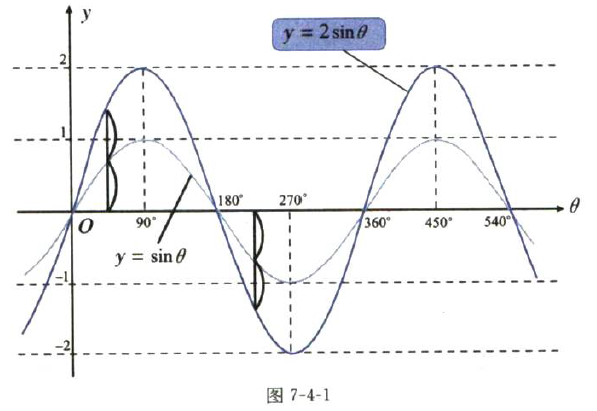
仔细观察这两个图象，就会发现有无系数2不会改变函数的周期。
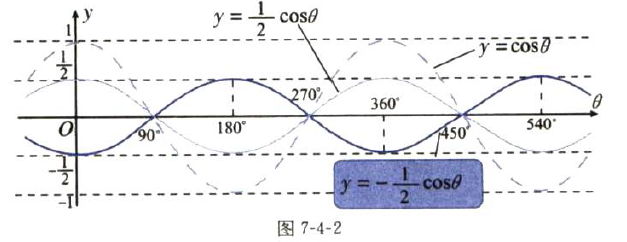
例子2： y=1/2*cosθ和y=-1/2*cosθ
通常，函数y=asinθ中，|a|就表示表示振幅。y=acosθ也同样如此。
因为振幅都是正数，所以需要用系数的绝对值来表示。本题中，先把y=cosθ的图象沿着y轴缩短到原来的1/2，就得到了y=1/2*cosθ的图象，又因为系数a=-1/2<0，所以y=1/2cosθ的图象上下颠倒一下，就得到了y=1/2*cosθ的图象。
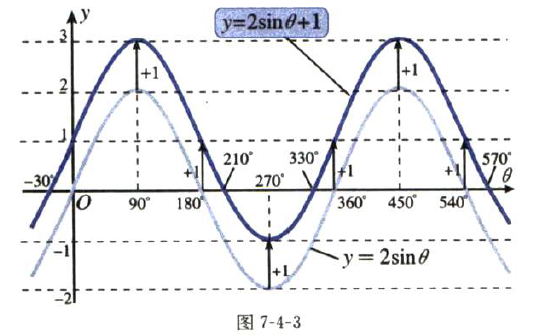
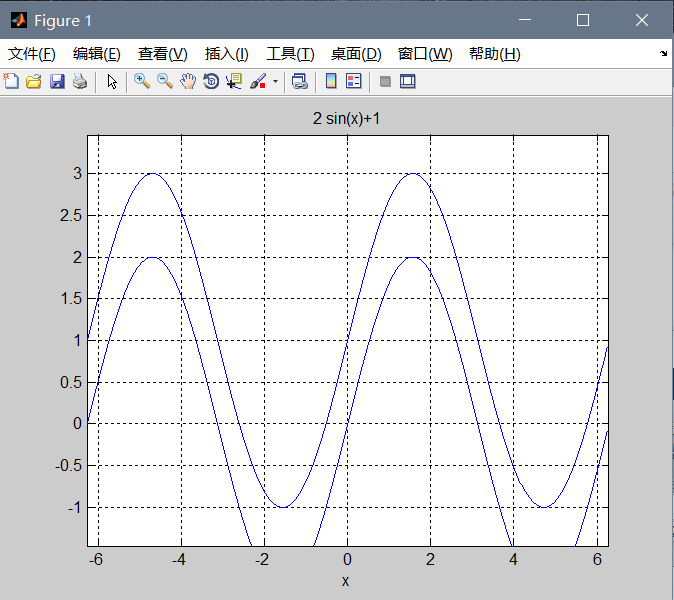
例3：函数y=2sinθ+1的图象是怎么样的？
即，有无常数项+1对图象的高度有什么影响呢？
如下图所示。
在物理学中，波所蕴涵的能量与振幅的平方成正比。也就是说，当波的振幅变为原来的两倍时，它的能量就变为原来的4倍；而当振幅变为3倍时，能量就变为9倍。
例如，1m高的波浪看似没有什么能量，但如果变为3m高，它所蕴涵的能量就远远超过你的想象了（是1m浪高所蕴涵能量的9倍)。
勇哥用Matlab画示例2的图象如下：
ezplot('-1/2*cos(x)')
grid on
hold on
ezplot('1/2*cos(x)')
hold on
ezplot('cos(x)')
同样的方式，得到了示例3的图象：
---------------------
作者：hackpig
来源：www.skcircle.com
版权声明：本文为博主原创文章，转载请附上博文链接！
本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：
